This post describes the paper that I recently published in the International Journal of Production Economics with Jeffrey Smith and Kevin Gue on deigning layouts for block stacking warehouses. You can download the paper from here or access it from the journal website, here.
When it comes to design a layout for block stacking warehouses, most of the existing models focus on determining the lane depth with respect to space utilization and do not consider material handling costs. Several analytical models exist that formulate space utilization as a function of lane depth and obtain the optimal lane depth that maximizes space utilization [1]-[4]. Developing a similar model for material handling cost is very difficult because forklifts are usually operated in block stacking storage areas under continuous multi-command pick-up/drop-off operations, where vehicles (pickers) perform replenishment and retrieval operations continuously one after another before heading back to their home/parking. Hence, formulating the total transportation cost as a function of lane depth depends on the sequence of the retrieval and replenishment operations and their assignments to the vehicles, which are unknown in advance and vary every day. Simulation appears to be an excellent tool to model the dynamics of the material handling in such a system and to obtain a realistic estimate for material handling costs. For this reason, we developed a simulation-based optimization approach to find the layouts that minimize both space and material handling costs using simulation to evaluate potential solutions.

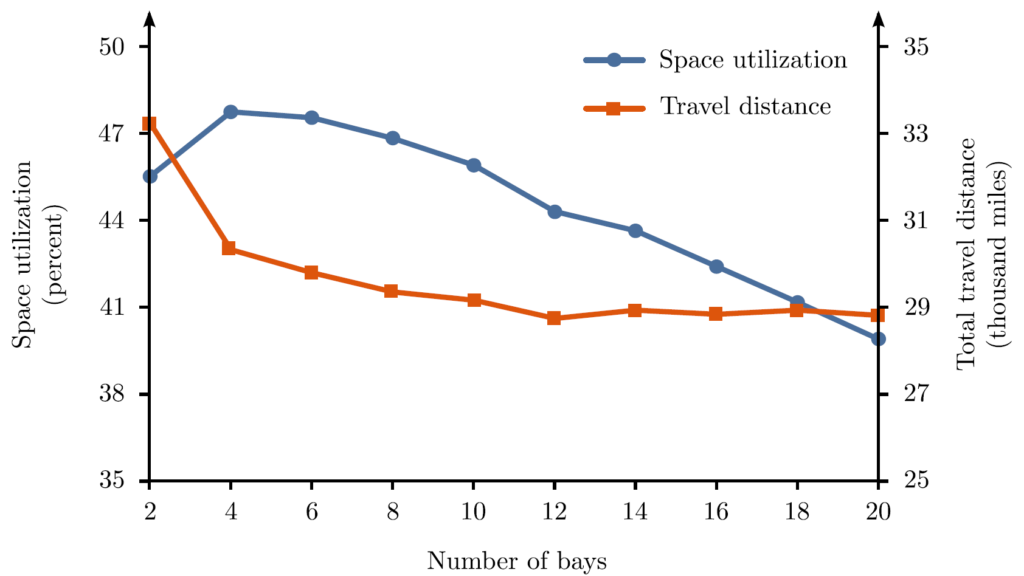
To the best of our knowledge, no commercial simulation package offers a flexible enough structure to simulate and evaluate several block stacking layouts generated by an optimization algorithm. Hence, for the first step, we developed an event-based simulation model in Python that takes layout-related parameters such as layout size, the number of bays and their depths, production and depletion rates (or logs) and safety stock levels for each SKU, and the number of forklifts and produces performance metrics related to space and material handling costs. Figure 1 presents a typical block stacking layout we assumed in the simulation model. The details of the simulation model are described in the paper that Jeff Smith, Kevin Gue, and I published in the Progress in Material Handling Research: 2016 [5]. The paper is open access and can be downloaded from this link. One of our main findings through an experimental study with the simulation model was that there was a trade-off between the material handling cost and space utilization with respect to bay depths (see Figure 2). Our experiments showed that space utilization increases as the number of aisles increases (i.e., bay depths decrease because the warehouse size is fixed) until it reaches its maximum. Then, it declines as bay depths become shallower (because of an increase in accessibility waste) while the material handling costs (i.e., the total travel distance by vehicles) improve; however, the improvement in material handling costs becomes modest after a certain point. Hence, transportation costs improve at the expense of lower space utilization.
We used the simulation model in a simulation-based optimization algorithm to design the entire layout of a block stacking warehouse. Our model finds the optimal number of aisles and cross-aisles, cross-aisle type (unidirectional vs. bidirectional), and bay depths that minimize space and material handling costs. We developed various analytical models to find the lower and upper bounds for the number of aisles and cross-aisles in the potentially good solutions to restrict the simulation efforts to only potentially optimal alternatives efficiently. These models include a closed-form solution model to find the optimal number of aisles maximizing space utilization. Assuming a common bay depth in the warehouse, the optimal number of aisles is
![]()
where Sl and Sw are the warehouse length and width (in units of pallets), respectively, Ns is the number of SKUs stored in the warehouse, and A is the aisle width (in units of pallets). Consequently, the optimal common bay depth in the warehouse is obtained by Consequently, the optimal common bay depth in the warehouse is obtained by
![]()
This model differs from the existing lane depth model [1]-[3] in that it appropriately considers the waste of space imposed by dedicated area to aisles (i.e., accessibility waste) for the entire planning horizon and not only for the time that lanes are occupied (for more explanation, please see the previous post).
The outcome of the model is a Pareto frontier with respect to two objectives: space cost, and the material handling cost. We quantified the former objectives by the percentage of wasted space in the warehouse and the latter objective by the required number of forklifts. This was to simplify converting solutions to their equivalent dollar amounts.
Our exhausting experimental study on test problems with different sizes showed that our model is capable of finding the Pareto frontier in a reasonable time for large-sized problems (less than 5 hours for a problem with 1000 SKUs). Figure 3 shows a Pareto frontier our model obtained for a test problem with 1000 SKUs. The paper contains several insights into the layout design problem that we obtained from our experimental study.
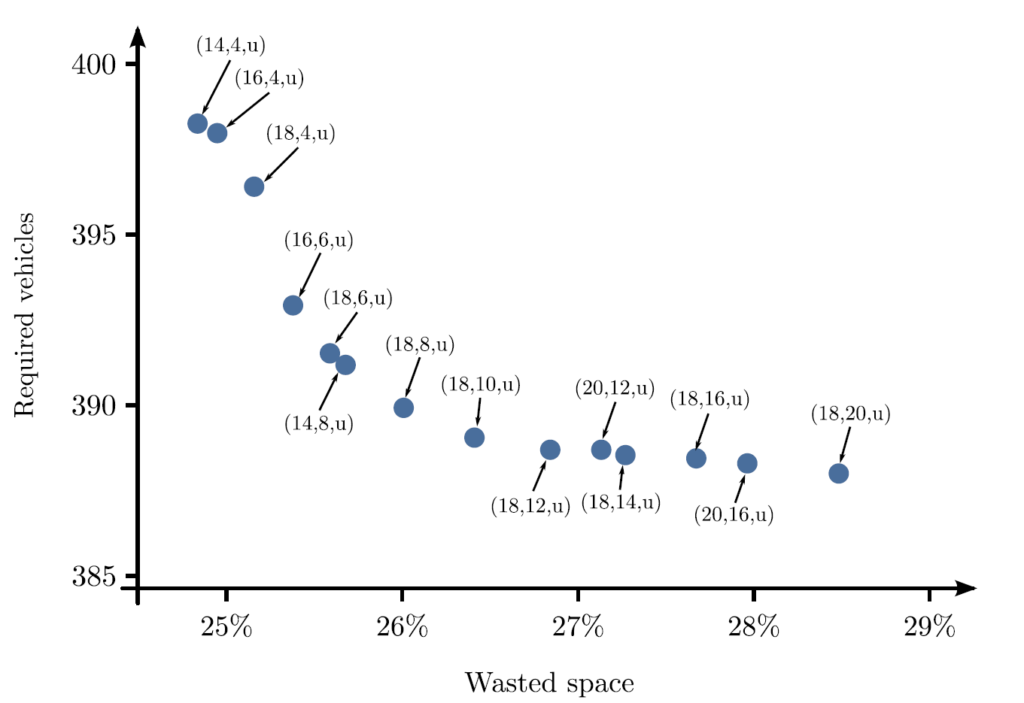
solutions format: (# of aisles, # of cross-aisles, cross-aisles type).
The results of implementing our model for a case of bottled beverages showed that considering both space and material handling costs in designing the warehouse layout could lead to saving more than half a million dollars annually on the total operational costs of a warehouse (see Figure 4).
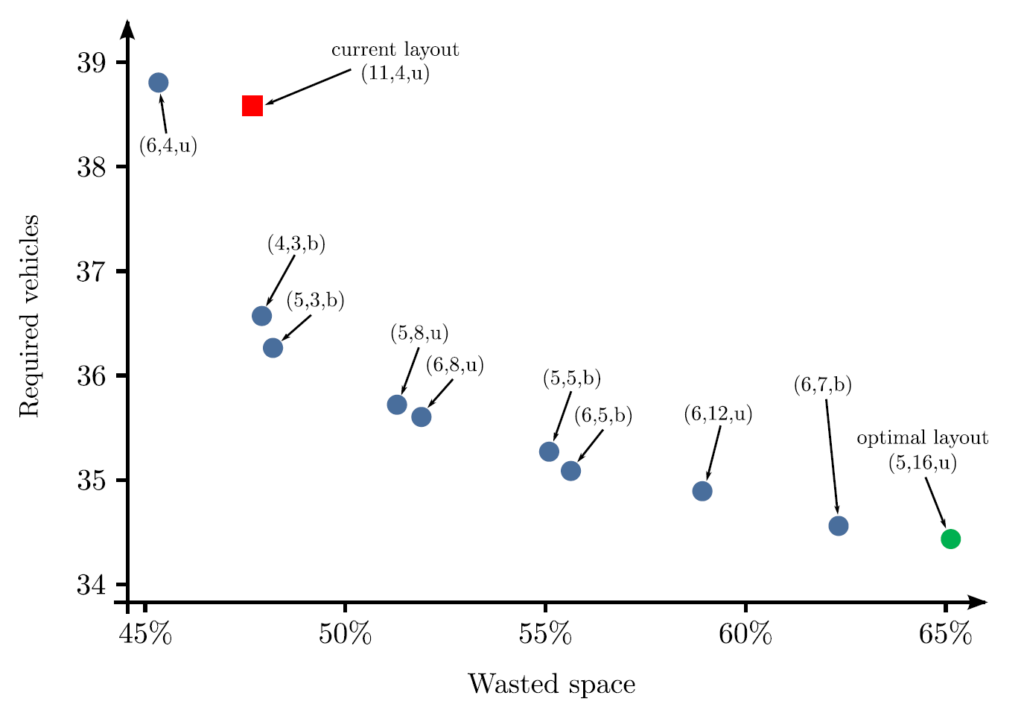
solutions format: (# of aisles, # of cross-aisles, cross-aisles type).
References:
- Kind, D. A. (1975). Elements of Space Utilization. Transportation and Distribution Management, 15, 29–34.
- Matson, J. O. (1982). The Analysis of Selected Unit Load Storage Systems. PhD thesis, Georgia Institute of Technology, Atlanta, GA.
- Derhami, S., Smith, J.S., Gue, K.R. (2017). Optimising space utilisation in block stacking warehouses. International Journal of Productions Research, 55 (21), 6436–6452.
- Derhami, S., Smith, J.S., Gue, K.R. (2019). Space-efficient layouts for block stacking warehouses. IISE Transactions, 51 (9), 957–971.
- Derhami, S., Smith, J.S., Gue, K.R. (2016). A simulation model to evaluate the layout for block stacking warehouses. In: 14th IMHRC Proceedings: Progress in Material Handling Research: 2016, Karlsruhe, Germany.
