About more than a year ago, I published a paper with Jeffrey Smith and Kevin Gue in the International Journal of Production Research on the optimal lane depth for block stacking (the first of series of papers on block stacking extracted my Ph.D. dissertation). The paper can be downloaded from here and the journal website here.
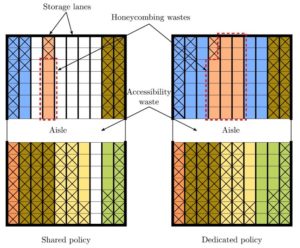
Block stacking is referred to storing pallets of Stock Keeping Units (SKUs) on top of one another in lanes on the warehouse floor. The fact that this storage system does not require racks or storage facility has made it very popular especially when pallets are heavy and large like SKUs in the bottled beverage and home appliance industries.

Block stacking is mostly operated under the shared (random) storage policy. Under this policy, once a lane is empty, it is available to all SKUs. However, to avoid blockage or pallet relocations, only pallets of the same SKU are allowed to be stored in the same lane. This renders some waste of storage space in the lanes as unoccupied pallet positions in a lane are not available to other SKUs. This effect is termed honeycombing, and waste associated with it remains until the lane is entirely emptied or occupied. Aisles also contribute to the waste of storage space because they are not directly used for storage though they are required to access lanes.
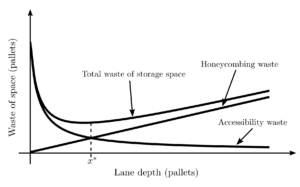
The traditional lane depth model (Kind 1975; Matson 1982) tries to minimize the total waste of storage space by finding the lane depth that optimizes the trade-off between honeycombing and accessibility waste. However, this model assumes infinite replenishment rate, which is only the case in warehouses receiving products from suppliers (a truck unloads a batch of pallets, and it is safe to assume pallets are stored instantaneously). This is not the case in warehouses located in manufacturing environments. We relaxed this assumption and obtained the model for finite replenishment rates.
For a set of N SKUs that are produced in batches of Qi pallets, stored by the rate of Pi pallets/hr, retrieved by the rate of λi pallets/hr, and stacked to Zi pallets, the optimal lane depth for the case that Pi > λi is
![]()
where A is the aisle width in units of pallets. If Pi < λi, the optimal lane depth is given by
![]()
and for Pi =∞, it is
![]()
One interesting fact we found about the optimal depth model was that the total waste of storage space as a function of lane depth behaves similar to the famous EOQ model.
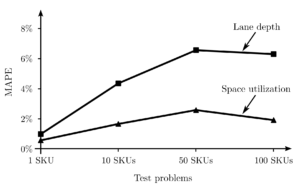
The lane depth model is derived using restrictive assumptions such as deterministic demand and production rates. We performed a simulation model and relaxed these assumptions to study the model under stochastic demand and production rates, and production batch sizes that usually exist in real-world situations. The results showed that the model produces near-optimal solutions under high variations applied to these parameters and produces an error of up to 7% for the optimal lane depth and 2% for space utilization.
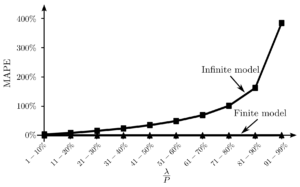
We also tested the traditional model (infinite replenishment rate) to estimate the optimal lane depth in a manufacturing warehouse where products are stored by finite production rates. The results showed that as the ratio of demand rate to the production rate increases, the error of the infinite model increases exponentially and reaches up to 400% overestimation of the optimal lane depth.
One of our main findings was that space utilization as a function of lane depth becomes smooth for depths deeper than the optimal lane depth. However, loss in space utilization becomes larger as the lane depth gets shallower than the optimal point. As a rule of thumb, one can say, when calculating the optimal lane depth is not possible, it is better from the space utilization point of view to have deep lanes rather than shallow lanes. However, this may impact material handling costs as the resulting solutions have fewer aisles and also vehicles have to travel longer distances to replenish/retrieve deeper lanes.
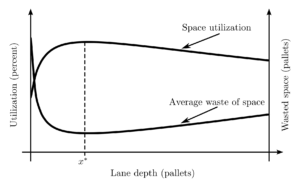
It is important to take into account that the lane depth model optimizes the trade-off between honeycombing and accessibility waste. It computes the accessibility waste for a lane only for the period that the lane is occupied and assumes dedicated space to an aisle is available for storage otherwise. That is, it underestimates accessibility waste when it comes to design a full layout with fixed aisles. Stay tuned for further research that addresses this issue.
References:
- Kind, D. A., “Elements of Space Utilization.” Transportation and Distribution Management, 15, 29–34, 1975.
- Matson, J. O., “The Analysis of Selected Unit Load Storage Systems.” PhD thesis, Georgia Institute of Technology, Atlanta, GA, 1982.
